
发布日期:2023-08-08 来源: 网络 阅读量()
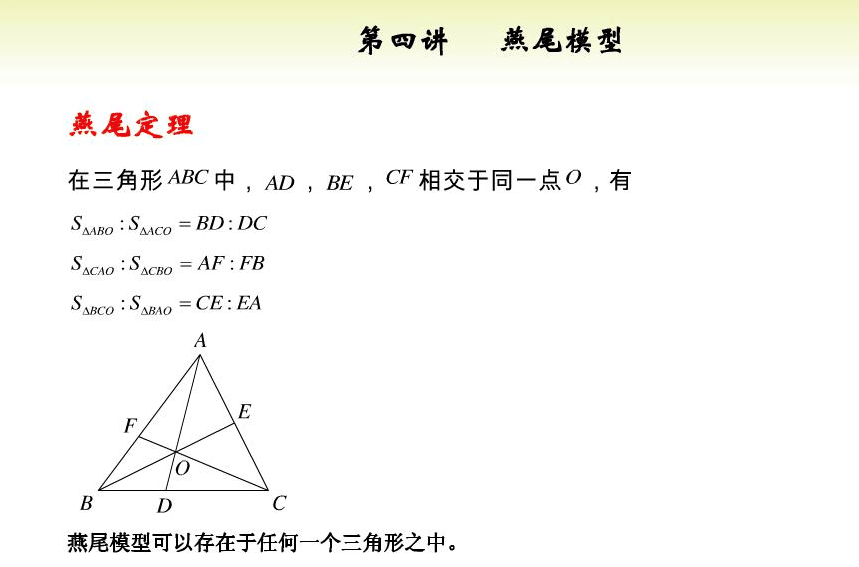
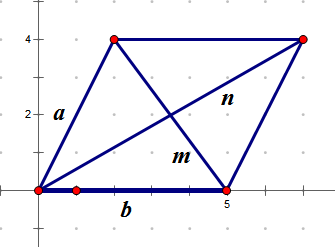
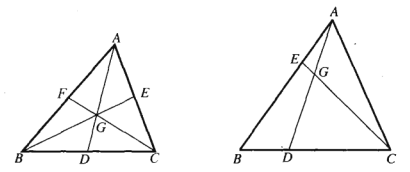
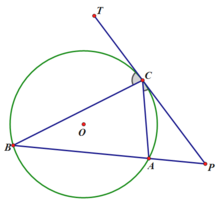
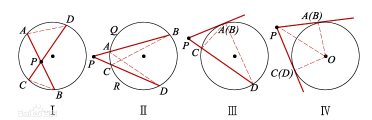
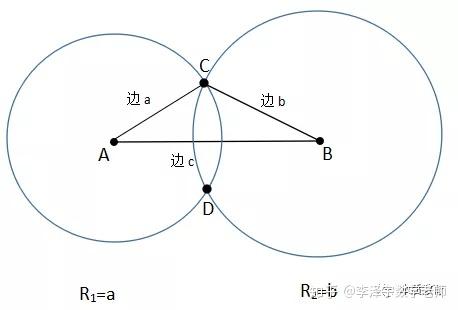
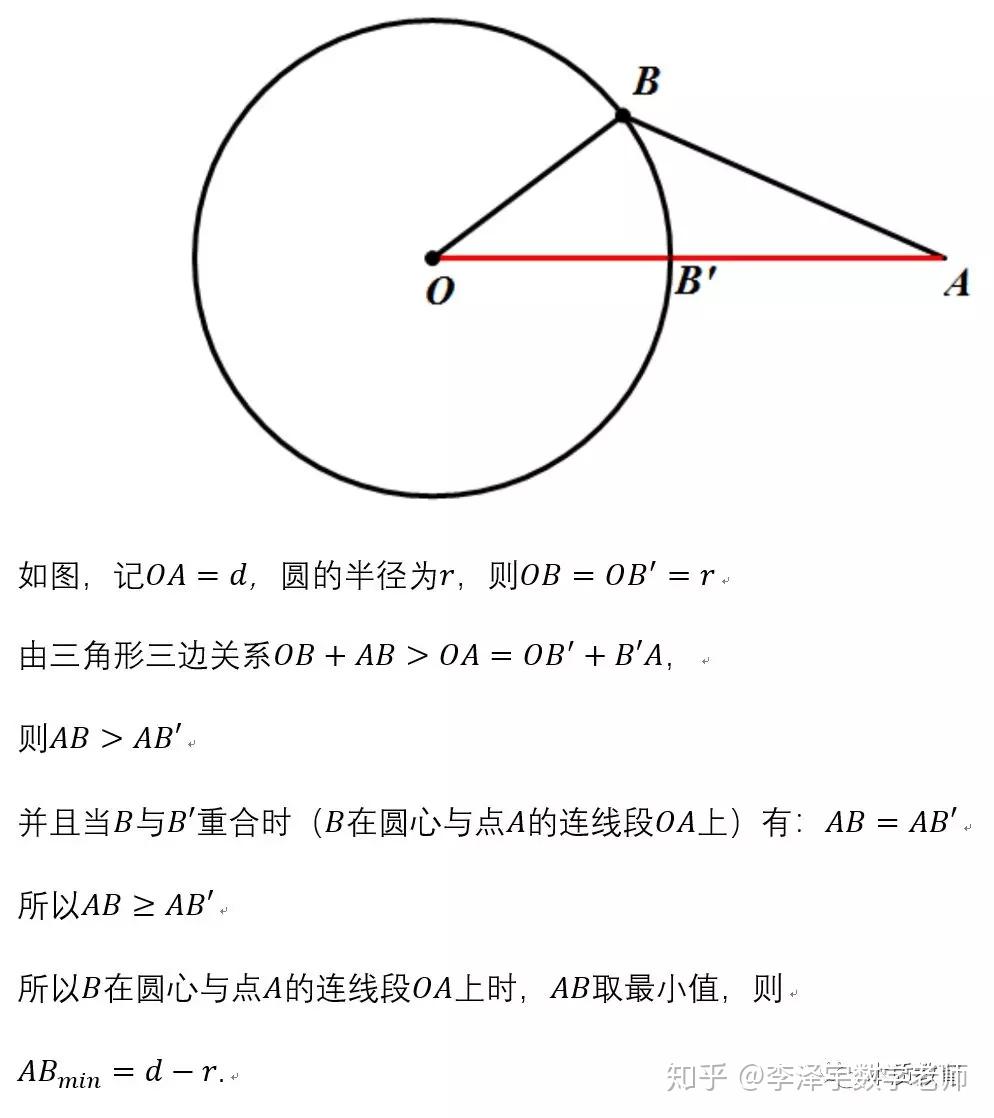
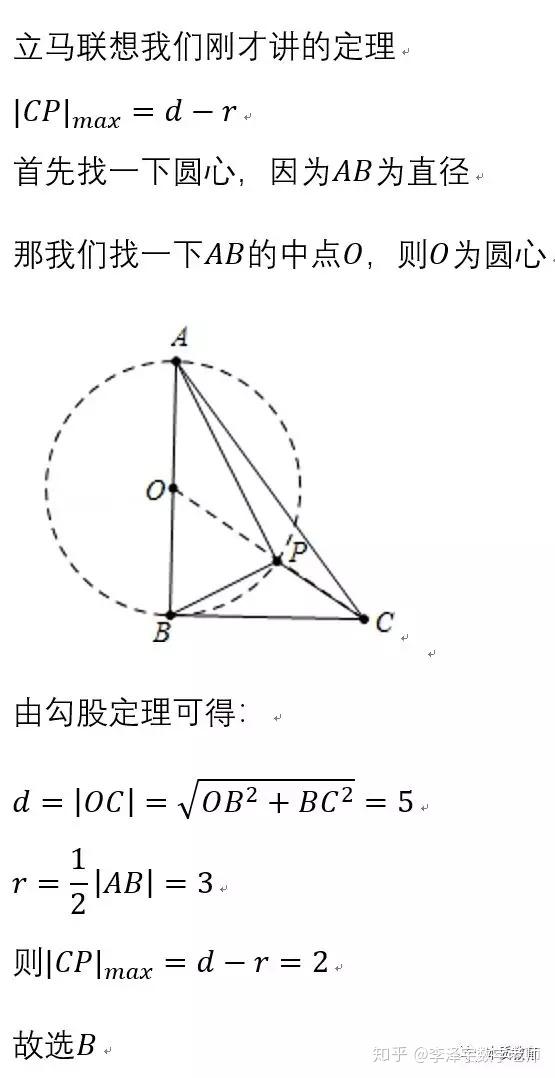
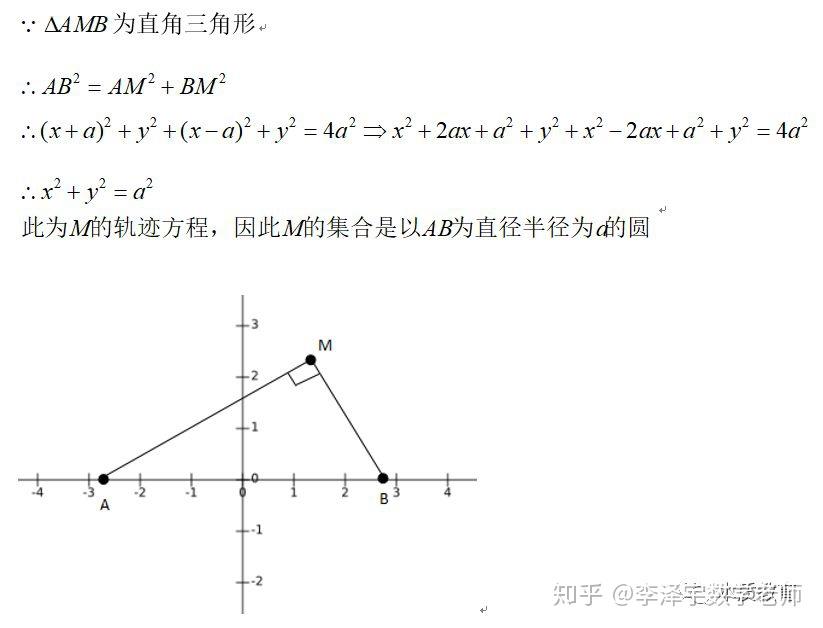
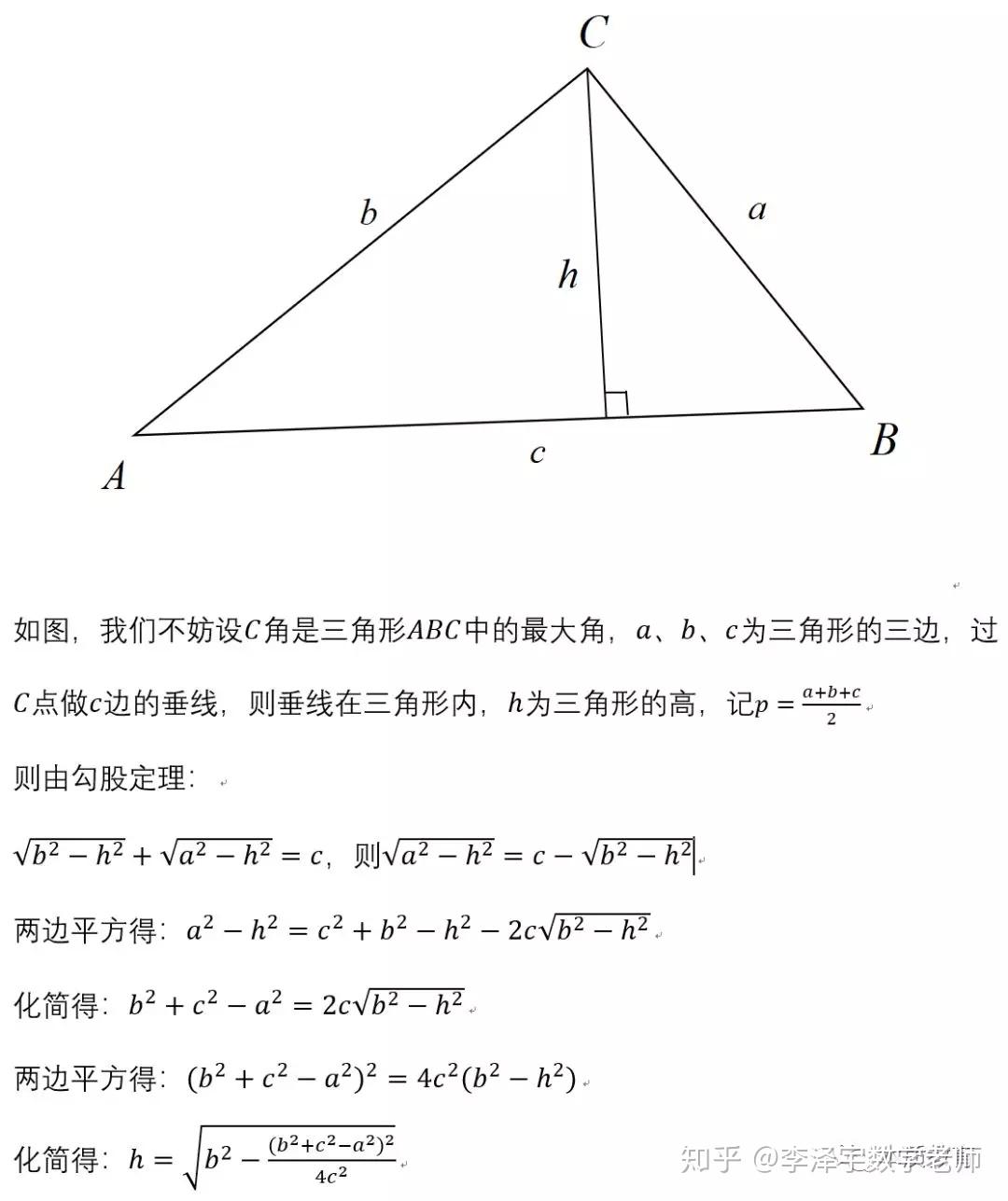
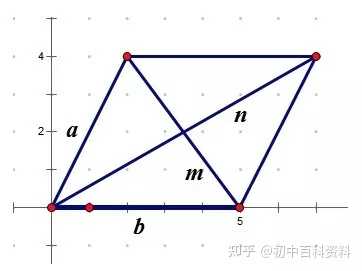
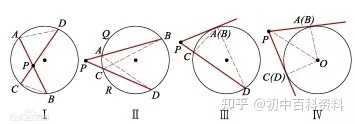
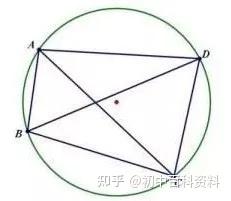
比如韦达定理、母子三角形边的公式等等。 坐标上海,教科书中都没有出现过,平时老师也是只是提到过。另外上海中考中综合题好像是能用拓展内容的。想知道填空、选择、解答题有哪些好用的定理、公式?或者高中学的,初中能用上的也可以_(:зゝ∠)_ 斯特瓦尔 塞瓦定理 燕尾定理 鸟头定理 鸡爪定理 蝴蝶定理 海伦定理 角平分线定理二 托勒密定理 费马点 斯特瓦尔特定理 西姆松定理 圆幂定理 中线定理 eqzx 塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 (BD/DC)×(CE/EA)×(AF/FB)=1。 蝴蝶定理视频http://v.youku.com/v_show/id_XMTkwODAwODQ=.html?x&sharefrom=android 以下是从中考数学的压轴题有什么快速运算的高中公式或技巧? - 知乎中摘出的与选择填空相关的内容。稍有改动,有兴趣可以到原答案查看。 一、代数篇 (1)立方公式:(实用度: ★ ) (2)头同尾合十:(实用度: ★ ★ ★ ) 名词解释: 例如28*22,两个两位数,十位数字2相同,个位数字8+2=10,故称头同尾合十。 巧算方法: 尾数相乘,得出的答案占后两位;头乘(头+1),占前一位到两位,就可以得出积。比如28*22,尾数相乘:2*8=16,2*(2+1)=6,依次排序就是616。 用法: 85*85,口算时,为8*(8+1)=72,5*5=25,一边算一边写就得出了答案7225。 47*45,口算时,折分成(45+2)*45来计算。45*45=2025,在脑子里对2025加上90,即得2115。 PS:这个是小学速算,本质是整式的乘法。小学时也学过不少别的技巧,不过感觉这个最实用,尤其是对于35^2,65^2之类,效果很好,初中高中都能用到,能省半分钟时间且没有算错的可能,也就没有了验算的麻烦。 二、几何篇 (1)平行四边形:(实用度: ★ ★ ) 两边长为a和b,两对角线长为m和n,则有 可以拿这个公式和托勒密定理对比记忆。 (2)三角形: A.勾股数:(实用度: ★ ★ ) 常见的最简勾股数有: 3、4、5 5、12、13 8、15、17 7、24、25 9、40、41 B.面积公式:(实用度: ★ ★ ) 利用两边及其夹角求面积。 PS:几何中的三角形面积公式只需要记这一个,其他的公式连竞赛都很难用得上。 C.三角恒等式:(实用度: ★ ) 这几个公式对于初中来说确实没什么用,很少能用到。不过如果有兴趣,记下来了,高中需要背的时候就会少一些麻烦。 D.正余弦定理:(实用度: ★ ★ ) 在遇到45度、60度、75度之类的非直角三角形题目时,我们可以用上这两个公式。其他时候很少能用得上。所以要记得: E.重心(质量法):(实用度: ★ ★ ★ ) 三角形的重心将中线分为2:1的两段。 质量法:(填空压轴题重点!!) 两个小球A、B,如果质量相等,如(1),那么它们的重心是AB的中点D。 如果质量不等,质量比为m/n,如(2),那么重心D仍在AB上,而AD/DB=n/m。(即杠杆原理) 如果三个质量相等(都等于1)的小球A、B、C构成三角形ABC要求它们的重心可以分为两步: 先求出B、C的重心,即B、C的中点D,可以用质量为2(=1+1)的小球放在D点,以取代B、C两个小球。 再求A、D的重心,由于D处的质量为2,A处的质量为1,所以重心G在AD上,且分AD为2:1(即AG:GD=2:1)。 下面,我们举一个简单的例子。 例:如图△ABC,AB上有一点E,BC上有一点D,AD交CE于点G,当AE:EB=1:2,BD:DC=1:2时,AG:GD等于多少? 解:我们在C处放质量为1的小球,B处放质量为2的小球,A处放质量为4的小球。此时AB、BC的重心E、D满足AE:EB=1:2,BD:DC=1:2。 我们将B、C的质量集中在D点,质量为3。A点质量为4。故AG:GD=3:4 同样如果需要,我们可以求得EG:GC=1:6 (3)圆: A.弦切角定理:(实用度: ★ ★ ) 解释:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 如图所示,线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。 定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数。 在上图中,我们有∠TCB=∠CAB、∠PCA=∠CBA B.圆幂定理:(实用度: ★ ★ ★) ①相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 如图I,即有AP·PB=CP·PD ②割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D, 如图II,即有PA·PB=PC·PD ③切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。 如图III,即有PA^2=PC·PD ④切线长定理:从圆外一点引圆的两条切线,它们的切线长相等。 如图IV,即有PA=PC C.托勒密定理:(实用度: ★ ★ ) 圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。 如图,即有AB·CD+AD·BC=AC·BD D.四点共圆:(实用度: ★ ★ ★ ) (填空压轴题重点!!) ①对角互补的四边形四点共圆。 ∠ADC+∠ABC=180度 ②一个角的对角等于其补角的四边形四点共圆。 ∠ADC=∠EBC ③同底、同侧且对底边张等角的四点共圆。 ∠ADB=∠ACB ④相交弦定理的逆定理。 AP·PC=BP·PD ⑤割线定理的逆定理。 PA·PB=PC·PD(图中未给出) ⑥托勒密定理的逆定理 AB·CD+AD·BC=AC·BD ⑦其他,如西姆松定理的逆定理等。 上述定理的核心之处就在于各个定理通过四点共圆和相似三角形联系在一起。我们举一个例子进行练习。 例:如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,连接AE、BE,∠BEC=60度,若AE=3,CE=7 ,则BE=________。 解: 因为△ABC为等边三角形, 所以∠BAC=∠BEC=60度, 所以A、E、B、C四点共圆 由托勒密定理可得:AB·CE=AC·BE+AE·BC, 因为AB=AC=BC, 所以CE=AE+BE, 所以BE=CE-AE=4 三、解析几何篇 (1)点线之间的距离:(实用度: ★ ★ ★ ) A.点与点: 对于点(x1,y1)和点(x2,y2),距离 B.点与线: 对于点(x0,y0)和线y=kx+b,距离 C.线与线: 对于线y=kx+b1和线y=kx+b2(注意k必须相等,即平行线才有距离),距离 (2)三角形的面积公式:(实用度: ★ ★ ★ ) 对于一个点在原点,另两个点分别为(x1,y1)和(x2,y2)的三角形面积为 有些同学在学习初中数学的时候感觉比较吃力,有点跟不上老师的步伐,不知道如何学好初中数学,原因是初中数学教材为了简化,部分公式及定理讲解不够全面,或者出现教材上没有讲,但是考试却考了的情况。导致同学们在考试过程中不能够很熟练的运用公式或定理快速解题。 一个良好的数学教材的定义:该教材可以由学生自学,即学生在没有老师的指导的情况下,自学教材可以获取考试所需的所有知识。 如何学好初中数学,本质教育有三个重要的要求: 通过我们详解下面一系列的公式,来帮助基础知识掌握得不错的同学在考试过程中更好的运用该公式,从而为我们学好初中数学走好第一步。 很遗憾,这一部分在初中教材中缺失,但考试却会用到 由此公理,我们可以推出3个不等式的性质,并且可以用公理进行证明 从证明过程我们也可以发现,如果我们掌握了不等式的公理以及证明过程,那么很多不等式的题目我们就可以直接求解,减少考试时遇到这类题目想办法去证明二级结论的时间,从而加快解题速度。 如何学好初中数学:教材公式拓展-实战演示 学会这个公式前因后果,我们就能多一条翻译的路径,可简化很多繁琐的运算,即可迅速解出答案,如果是在考试中就能大幅提高解题速度,提高考试成绩,学好初中数学。 定理:若存在三条边,其任意两边之和大于第三边,则这三条边必定可以构成三角形 初中教材给出了三角形三边的关系: 三角形的两边之和大于第三边. 实际上该命题的条件对于结论来说不仅是充分的而且还是必要的.即是说上面命题的逆命题也是成立的,遗憾的是课本并未指明,然而中考题里却出现了要使用其逆命题的题目 这个定理等价于:若三条边满足最短两边之和大于第三边,那么这三边可以构成一个三角形。 也等价于:若三条边满足最长边和最短边之差小于第三边,那么这三边可以构成一个三角形 证明: 即证明出等价定理:若三条边满足最短两边之和大于第三边,那么这三边可以构成一个三角形。 从证明过程我们也可以发现,如果我们掌握了构成三角形三边长的关系公理以及证明过程,那么很多判断能否构成三角形的题目我们就可以直接求解,减少考试时遇到这类题目想办法去证明二级结论的时间,从而加快解题速度。 例题(2015秋?鄂城区校级月考) 将长为15cm的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有( ) A.5种 B.6种 C.7种 D.8种 解析: 3: 如何学好初中数学:教材公式拓展-圆外一点到圆上的点的最值公式及其证明 初中教材只讲解了圆外的点和圆的位置关系,而中考里常出现圆外一点或直线到圆上点距离的最值问题,如果不知道这个定理,那么将无法下手解题。掌握了这个公式的话,在高考中也能用到,可谓一石二鸟。 怎么记忆呢? 证明: (应用到我们上一篇文章三角形三边关系): 如何学好初中数学:教材公式拓展-实战演示 例题 解析: 第一步,直接把题目里面的已知结合我们学过的知识化简一下: 接下来, 应用本质教育数学三招第三招盯住目标 目标相当于是求圆外一定点到圆上一点距离的最小值 4: 如何学好初中数学:教材公式拓展-平面内两定点连线互相垂直的点的轨迹是圆及其证明。 很遗憾,这个定理在初中教材中没有提到,但考试却会用到。教材中讲到的圆的性质中,讲到直径所对应的圆心角是90度。这个定理便是由这条性质衍生而来。 证明: 证明此定理: 在平面内两定点AB,点M与AB两点的连线AM,BM互相垂直 以AB的中点为原点,以AB为X轴,设AB的长度为2a。 因此A的坐标为(-a,0),B的坐标为(a,0)。 设M点的坐标为(x,y) 如何学好初中数学:教材公式拓展-实战演示 例题 解析: 如何学好初中数学:教材公式拓展-海伦公式及其证明 以前老版本的教材中是有这个公式的,但是新版本的已经没有了。掌握了这个公式的话,在中考甚至高考中都能用到,只要知道三角形三边即可求出面积省去了很多步骤。 证明: 如何学好初中数学:教材公式拓展-实战演示 解析: 第二问,利用本质教育 李泽宇三招?第三招盯住目标,由题目的已知可以把三角形的三边都表示出来,从而可以想到利用海伦公式快速表示出三角形面积 (感兴趣的同学可以搜一搜标准答案,无非就是将我们的证明过程写一遍,很繁琐的化简,因为初中没有学过正余弦定理,所以记住海伦公式对提高解题速度帮助还是挺大的) 结论 学会上述这些定理的前因后果,我们就能迅速解决相关的填空选择题甚至大题,即可迅速解出答案,如果是在考试中就能大幅提高解题速度,提高考试成绩,学好初中数学。 射影定理必须榜上有名,现在大部分地区教材上虽然删掉了,但是解中考小题简直如有神助。 感谢邀请,我直入主题啦。 立方公式(实用度:★) 头同尾合十(实用度:★ ★ ★ ) 名词解释 例如28*22,两个两位数,十位数字2相同,个位数字8+2=10,故称头同尾合十。 巧算方法 尾数相乘,得出的答案占后两位;头乘(头+1),占前一位到两位,就可以得出积。比如28*22,尾数相乘:2*8=16,2*(2+1)=6,依次排序就是616。 用法 85*85,口算时,为8*(8+1)=72,5*5=25,一边算一边写就得出了答案7225。 47*45,口算时,折分成(45+2)*45来计算。45*45=2025,在脑子里对2025加上90,即得2115。 PS:这个是小学速算,本质是整式的乘法。小学时也学过不少别的技巧,不过感觉这个最实用,尤其是对于35^2,65^2之类,效果很好,初中高中都能用到,能省半分钟时间且没有算错的可能,也就没有了验算的麻烦。 平行四边形(实用度:★ ★ ) 两边长为a和b,两对角线长为m和n,则有可以拿这个公式和托勒密定理对比记忆。 三角形 A.勾股数(实用度:★ ★ ) 常见的最简勾股数有: 3、4、5 5、12、13 8、15、17 7、24、25 9、40、41 B.面积公式(实用度:★ ★ ) 利用两边及其夹角求面积。 PS:几何中的三角形面积公式只需要记这一个,其他的公式连竞赛都很难用得上。 C.三角恒等式(实用度:★ ) 这几个公式对于初中来说确实没什么用,很少能用到。不过如果有兴趣,记下来了,高中需要背的时候就会少一些麻烦。 D.正余弦定理(实用度:★ ★ ) 在遇到45度、60度、75度之类的非直角三角形题目时,我们可以用上这两个公式。其他时候很少能用得上。所以要记得: E.重心(质量法)(实用度:★ ★ ★ ) 三角形的重心将中线分为2:1的两段。 质量法:(填空压轴题重点!!) 两个小球A、B,如果质量相等,如(1),那么它们的重心是AB的中点D。 如果质量不等,质量比为m/n,如(2),那么重心D仍在AB上,而AD/DB=n/m。(即杠杆原理) 如果三个质量相等(都等于1)的小球A、B、C构成三角形ABC要求它们的重心可以分为两步: 先求出B、C的重心,即B、C的中点D,可以用质量为2(=1+1)的小球放在D点,以取代B、C两个小球。 再求A、D的重心,由于D处的质量为2,A处的质量为1,所以重心G在AD上,且分AD为2:1(即AG:GD=2:1)。 A.弦切角定理(实用度:★ ★ ) 解释:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角。 如图所示,线段PT所在的直线切圆O于点C,BC、AC为圆O的弦,∠TCB、∠TCA、∠PCA、∠PCB都为弦切角。 定理:弦切角的度数等于它所夹的弧所对的圆心角度数的一半,等于它所夹的弧所对的圆周角度数。 在上图中,我们有∠TCB=∠CAB、∠PCA=∠CBA B.圆幂定理(实用度:★ ★ ★) 相交弦定理、割线定理、切割线定理、切线长定理的统称。 ①相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 如图I,即有AP·PB=CP·PD ②割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D, 如图II,即有PA·PB=PC·PD ③切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。 如图III,即有PA^2=PC·PD ④切线长定理:从圆外一点引圆的两条切线,它们的切线长相等。 如图IV,即有PA=PC C.托勒密定理(实用度:★ ★ ) 圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。 如图,即有AB·CD+AD·BC=AC·BD D.四点共圆(实用度:★ ★ ★ ) (填空压轴题重点!!) ①对角互补的四边形四点共圆。∠ADC+∠ABC=180度 ②一个角的对角等于其补角的四边形四点共圆。∠ADC=∠EBC ③同底、同侧且对底边张等角的四点共圆。∠ADB=∠ACB ④相交弦定理的逆定理。AP·PC=BP·PD ⑤割线定理的逆定理。PA·PB=PC·PD(图中未给出) ⑥托勒密定理的逆定理AB·CD+AD·BC=AC·BD ⑦其他,如西姆松定理的逆定理等。 上述定理的核心之处就在于各个定理通过四点共圆和相似三角形联系在一起。我们举一个例子进行练习。 解: 点线之间的距离(实用度:★ ★ ★ ) A.点与点: 对于点(x1,y1)和点(x2,y2),距离 B.点与线: 对于点(x0,y0)和线y=kx+b,距离 C.线与线: 对于线y=kx+b1和线y=kx+b2(注意k必须相等,即平行线才有距离),距离 三角形的面积公式(实用度:★ ★ ★ ) 对于一个点在原点,另两个点分别为(x1,y1)和(x2,y2)的三角形面积为 正如毛主席所说:“我们既要在战略上要藐视敌人,也要在战术上要重视敌人!” 因此我也关注到了大家短期“战术”上的问题, 为大家系统的整理了初中相关的学习资料以及学习技巧,并创立了相关资料群, 下面便是部分截图展示: 前方多图来袭!但干货满满,文末有获取方式 初中数学所有知识点汇总 初中数学最全公式 初一到初三知识点汇总 部分文件 以上就是【初中数学】复习汇总和群文件部分资料截图了!希望对大家有帮助!! 天赋决定上限,努力决定下限。年轻人请努力,让自己出色,从能力到容貌。别让怯弱否定了自己,别让懒惰耽误了青春! 由于篇幅有限,只能展示这么多了! 祝大家能取得优异成绩! (码字不易,请大家点个赞,给予我持续输出的的动力!)再次谢谢大家观看此文。 关注我,将持续毫无保留的分享我的学习技巧以及资料,陪你逆袭,伴你成长! 一个拥有诸多学习心得和秘籍 以及初中所有科目复习资料 全网最全最优质的初中复习资料的硬核学长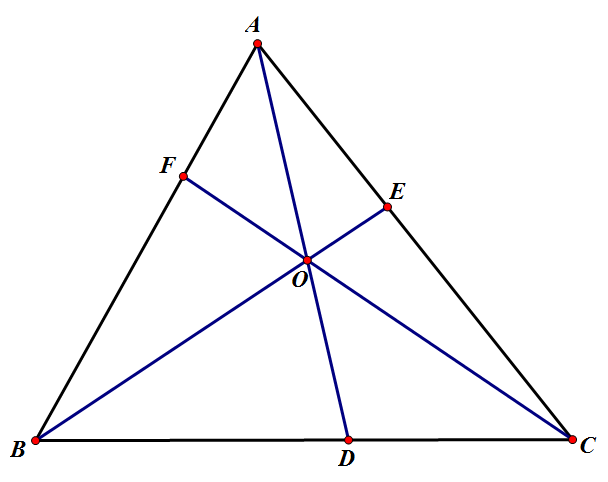
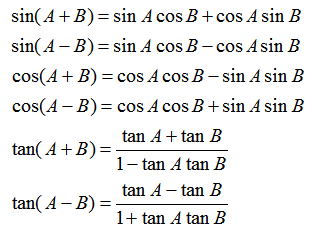

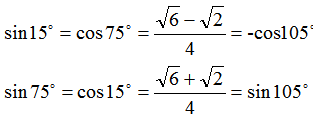
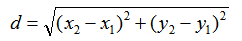
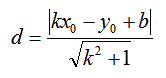
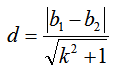
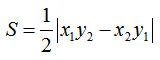
一,巩固基础知识,简单的题目做得又快又对,有时间思考难题;
二,学习数学三招,有逻辑地思考那些难题;
三,改掉错误习惯,减少运算错误、看错题目等毛病。要学好数学 - 除了打牢基础,最关键的就是数学思维 - 千变万化的题型背后不变的思维规律, 掌握了思维,才能做到灵活高效学习。 我专门把高中数学课本基础知识+定义+数学思维方法 用思维导导图的形式加以总结,方便同学们学习巩固, 如有需要: 直接戳下面卡片【联系试听我亲自授课的初/高中数学提高课】: 或获取如下图所示的资料
试听或下载高中数学所有基础知识总结思维导图及二级公式





结论 
















这里是初中百科资料,愿你深读。


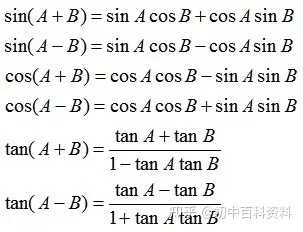

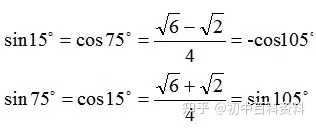

下面,我们举一个简单的例子。
例:如图△ABC,AB上有一点E,BC上有一点D,AD交CE于点G,当AE:EB=1:2,BD:DC=1:2时,AG:GD等于多少?
解:我们在C处放质量为1的小球,B处放质量为2的小球,A处放质量为4的小球。此时AB、BC的重心E、D满足AE:EB=1:2,BD:DC=1:2。
我们将B、C的质量集中在D点,质量为3。A点质量为4。故AG:GD=3:4
同样如果需要,我们可以求得EG:GC=1:6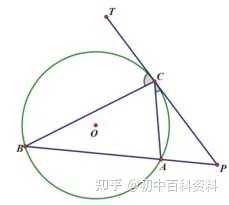
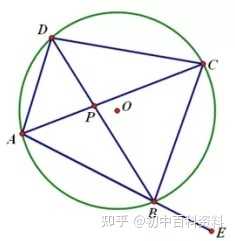
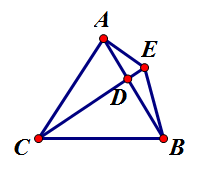
例:如图,△ABC为等边三角形,D为AB上一点,点E为CD延长线上一点,连接AE、BE,∠BEC=60度,若AE=3,CE=7 ,则BE=________。

因为△ABC为等边三角形,
所以∠BAC=∠BEC=60度,
所以A、E、B、C四点共圆
由托勒密定理可得:AB·CE=AC·BE+AE·BC,
因为AB=AC=BC,
所以CE=AE+BE,
所以BE=CE-AE=4
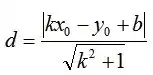

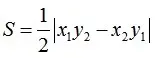


















部分素材源于网络,侵删