【重点】最优化计算与matlab实现（20）——遗传算法

杏鑫资讯

公司新闻

行业动态

技术资讯

公司新闻

【重点】最优化计算与matlab实现（20）——遗传算法

发布日期：2024-03-11 来源: 网络阅读量（）

《精通MATLAB最优化计算（第二版）》

Matlab 2019a

石中居士：最优化计算与Matlab实现——目录

遗传算法（也称为遗传优化算法）本质上是一种进化算法，它在很多领域都有广泛的应用，例如生产调度问题、自动控制、机器人学、图像处理和机器学习等。

遗传算法基于自然选择的生物进化，是一种模仿生物进化过程的随机方法。遗传算法是从代表问题可能潜在解集的一个种群开始，而一个种群则由经过基因编码的一定数目的个体组成，每个个体实际上是带有染色体特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体形状的外部表现。

在一开始需要实现从表现型到基因型的映射，即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解。

在每一代，根据问题域中个体的适应度大小挑选个体，并借助于遗传学的遗传算子进行组合交又和变异，产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样，后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

遗传算法包括三个基本操作：选择、交叉和变异，这些基本操作又有许多不同的方法。

1.选择

选择的含义为确定重组或交叉个体，以及被选个体将产生多少个子代个体。选择的标准一般是按照适应度来进行的，适应度的计算有以下两种方法：

（1）按比例的适应度计算；

（2）基于排序的适应度计算。

适应度计算之后是实际的选择，按照适应度进行父代个体的选择，可以挑选以下的算法:

（1）轮盘赌选择；

（2）随机遍历抽样；

（3）局部选择；

（4）截断选择；

（5）锦标赛选择。

2.交叉

交叉是结合来自父代交配种群中的信息，产生新的个体。依据个体编码表示方法的不同，可以有以下的算法：

（1）实值重组

离散重组
中间重组
线性重组
扩展线性重组

（2）二进制交叉

单点交叉
多点交叉
均匀交叉
洗牌交叉
缩小代理交叉

3.变异

交叉之后子代经历的变异，实际上是子代基因按小概率扰动产生的变化。依据个体编码表示方法的不同，可以有以下的算法：

（1）实值变异；

（2）二进制变异。

原理

下面给出的基本遗传算法程序用来求函数的最大值，它采用如下参数：

（1）用二进制编码来离散自变量，码长根据离散精度来确定，例如自变量的变化区间为 $[-10,10]$ ，当离散精度为 $0.01$ 时，码长为 $\\log _{2}\\{[10-(-10)]/ 0.01+1\\}=11$ ，即每个个体用 $11$ 位的二进制表示。

（2）交叉方法采用单点交叉，例如对于下面的两个个体：

如果切点在第4位，则通过交叉后，两个个体分别变为：

（3）变异是根据变异概率反转子代某个位的值，例如将0变成1，一般变异概率为很小的数，在0到0.05之间。

（4）选择策略采用轮盘赌策略，令 $P P_{i}=\\sum_{j=1}^{i}p_{i}, \\quad P P_{0}=0$ ，其中 $P P_{i}$ 为累计概率， $p_{i}$ 为个体的选择概率，其计算公式为： $p_{i}=\\frac{\ ext{ fitness }\\left(x_{i}\\right)}{\\sum_{i=1}^{N P}\ ext{ fitness }\\left(x_{i}\\right)}$ ，其中 $\\mathrm{fitness}\\left(x_{i}\\right)$ 为个体的适应度。共转轮 $NP$ 次（ $NP$ 为种群个体数），每次转轮，随机产生 $0$ 到 $1$ 之间的随机数 $r$ ，当 $P P_{i-1}\\leqslant r<P P_{i}$ 时选择个体 $i$ 。

从选择概率的计算公式可以看出，个体的适应值越大，其选择概率越大，因此如果将目标函数作为适应函数，则此遗传算法是求目标函数的最大值。

算法步骤

基本遗传算法的基本步骤如下：

【1】随机产生初始种群，个体数目一定、每个个体表示为染色体的基因编码；

【2】用轮盘赌策略确定个体的适应度，并判断是否符合优化准则，若符合，输出最佳个体及其代表的最优解，并结束计算，否则转向【3】；

【3】依据适应度选择再生个体，适应度高的个体被选中的概率高，适应度低的个体可能被淘汰；

【4】按照一定的交叉概率和交叉方法、生成新的个体；

【5】按照一定的变异概率和变异方法，生成新的个体；

【6】由交叉和变异产生新一代的种群，返回到【2】。

Matlab代码与试算

用基本遗传算法求下面函数的最大值

$f(x)=x^{3}-60 x^{2}+900 x+100, \\quad 0 \\leqslant x \\leqslant 30$

个体数目取50，最大进化代数取100，离散精度取0.01，杂交概率取0.9，变异概率取0.04。

fitness.m

function F = fitness(x)
F = x^3 - 60*x^2 + 900*x + 100;

test.m

[x_optimization,f_optimization] = Genetic_Algorithm(@fitness,0,30,50,100,0.9,0.04,0.01);
x_optimization
f_optimization

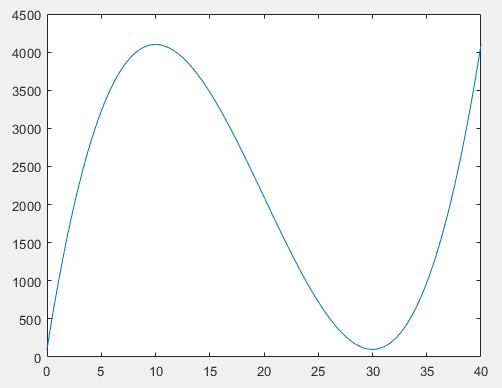
t = 0:0.01:40;
St = t.^3 - 60.*t.^2 + 900.*t + 100;
figure(1)
plot(t,St);

Genetic_Algorithm.m

function [x_optimization,f_optimization]= Genetic_Algorithm(fitness,a,b,Individual_Number,Evolution_Generation_Number,P_Hybrid,P_Mutation,epsilon)
%   fitness：待优化的目标函数
%   a：自变量下界
%   b：自变量上界
%   Individual_Number：种群个体数
%   Evolution_Generation_Number：最大进化代数
%   P_Hybrid：杂交概率
%   P_Mutation：变异概率
%   epsilon：自变量离散精度
%   x_optimization：目标函数取最小值时的自变量值
%   f_optimization：目标函数的最小值
%%%%%%%%%%%【1】%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Encoding_Length = ceil(log2((b - a)/epsilon + 1));       %根据离散精度，确定二进制编码需要的码长
x = zeros(Individual_Number,Encoding_Length);
for i = 1:Individual_Number
    x(i,:) = Initial(Encoding_Length);                %种群初始化         
    fx(i) = fitness(Decimalization(a,b,x(i,:),Encoding_Length));  %个体适应值   Decimalization：十进制化
end
%%%%%%%%%%%%【2】%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for k = 1:Evolution_Generation_Number
    sum_fx = sum(fx);                %所有个体适应值之和
    Px_avg = fx/sum_fx;                   %所有个体适应值的平均值
    PPx = 0;
    PPx(1) = Px_avg(1);
    for i = 2:Individual_Number                        %用于轮盘赌策略的概率累加
        PPx(i) = PPx(i-1) + Px_avg(i); 
    end
    for i = 1:Individual_Number
        sita = rand();  
        for n = 1:Individual_Number
            if sita <= PPx(n)
                SelFather = n;           %根据轮盘赌策略确定的父亲
                break;
            end
        end
        SelMother = floor(rand()*(Individual_Number - 1)) + 1;  %随机选择母亲
        Intersection = floor(rand()*(Encoding_Length - 2)) + 1;     %随机确定交叉点
        r1 = rand();
        if r1 <= P_Hybrid                                     %交叉
            nx(i,1:Intersection) = x(SelFather,1:Intersection);
            nx(i,(Intersection + 1):Encoding_Length) = x(SelMother,(Intersection + 1):Encoding_Length);
            r2 = rand();
            if r2 <= P_Mutation                               %变异
                Mutation = round(rand()*(Encoding_Length - 1) + 1);
                nx(i,Mutation) = ~nx(i,Mutation);
            end
        else
            nx(i,:) = x(SelFather,:); 
        end
    end
    x = nx;
    for i = 1:Individual_Number
        fx(i) = fitness(Decimalization(a,b,x(i,:),Encoding_Length));   %子代适应值
    end
end
f_optimization = -inf;
for i = 1:Individual_Number
    fitx = fitness(Decimalization(a,b,x(i,:),Encoding_Length));
    if fitx > f_optimization
        f_optimization = fitx;                                %取个体中的最好值作为最终结果
        x_optimization = Decimalization(a,b,x(i,:),Encoding_Length);
    end
end
function result = Initial(length)         %初始化函数
for i=1:length  
    r = rand();
    result(i) = round(r);   
end

function y = Decimalization(a,b,x,L)         %二进制编码转换为十进制编码
base = 2.^((L-1):-1:0);
y = dot(base,x);
y = a + y*(b-a)/(2^L-1);

命令行窗口

x_optimization=9.824175824175825


f_optimization=4.099067140322543e+03

函数图像

遗传算法求得的结果的精度一方面与离散精度有关，另一方面与个体数目有关，离散精度决定了遗传算法能得到的最大精度，个体数目越大，求得的结果精度越有可能达到离散精度。

由于遗传算法本身的特点，每次用同样的参数也可能求出差别比较大的结果，因此遗传算法主要用来估计极值点的大致位置。

石中居士：最优化计算与Matlab实现——目录

【重点】最优化计算与matlab实现（20）——遗传算法

相关资讯

官方微信