发布日期:2024-03-12 来源: 网络 阅读量()
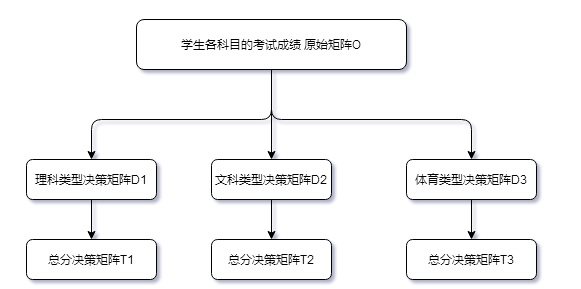
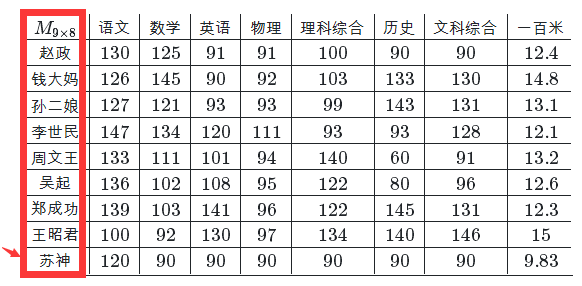
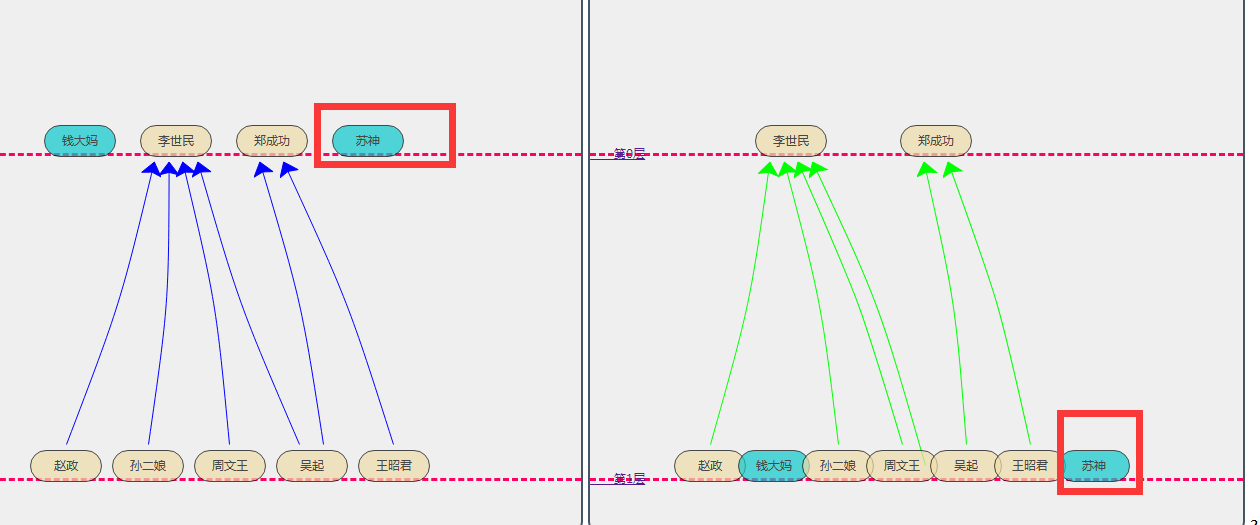
民数看书龟爬,知道一点拓扑,不懂图论,但公开课听着好像两个都一样啊!故有此一问,请大家不吝赐教! 图论研究的对象——「图」肯定是拓扑对象。 所谓「图」就是研究一个给定「顶点集」 一个「无向图」从拓扑的角度讲,是一系列一维胞腔粘贴的结果。 图论是欧拉为解决哥尼斯堡七桥问题研究最先引入,这也是拓扑学之肇始。从拓扑的角度讲,一个图中的顶点并不都一样,通过「度」这个概念可以进行分类。所谓「度」,就是指该顶点共有几条边与之相连。图论一般不关心「内点」,即非顶点的点。从同伦的角度讲,一个图的同伦型只取决于它有几个「圈」,或者说「洞」。对于无圈的图——「树」,它的图同伦于一个单点。 总之,拓扑研究的方向更具有一般性、抽象性。但是图论研究本身并不止步于此,而是向着优化、决策等算法方向发展。比如寻找最短路径等最优问题,而拓扑学家对此不再感兴趣。 图论是拓扑学的贫民窟。 “拓扑学”主要研究的是出于数学分析的需要而产生的 一些几何问题。 到现在来说,拓扑学主要研究拓扑空间,在拓扑变换下的不变性质和不变量。 图论( graph theoy)是数学的一个分支,它以图( graph)为研究对象,研究顶点(vertex)和边(edge,又称line) 组成的图形的数学理论和方法。图论中的图是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用顶点代表事物,用连接两顶点的边表示相应两个事物间具有这种关系。 图论的研究对象相当于“一维拓扑学”。 图论可以看成是拓扑学的一个子集。 下面是开始吹牛(装逼)的时间。 人们往往把研究的对象映射成一个结点,把结点跟结点之间的关系用线段来表示。并且把这些结点映射到几何空间,通过空间的几何形变,最终达到一个评价的目标。描述整个几何形变的过程就是可以用拓扑来表示。 举一个简单的例子,高考的选拔,其本质就是一种拓扑的表达。 上面是再常见的一个模型。 假定有9个学生。怎么评价哪个学生最好呢? 比如上面是体育类的评价结果。 上面是总分类得到的结果。 最后,图论就是拓扑的一个子集。 (或「节点集」)以及这些点的连接方式
,我们叫做「边」。边也可以有方向、权重等信息。