发布日期:2024-05-06 来源: 网络 阅读量()
目录 2.1SLSQP(Sequential Least SQuares Programming optimization algorithm) 2.2最小二乘最小化Least-squares minimization scipy api:https://docs.scipy.org/doc/scipy-0.18.1/reference/index.html 优化器optimize的参数设置:https://docs.scipy.org/doc/scipy-0.18.1/reference/optimize.html#module-scipy.optimize scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None) fun:目标函数,返回单值, x0:初始迭代点, method:求解方法 jac:目标函数的雅可比矩阵。可选的。仅适用于CG,BFGS,Newton-CG,L-BFGS-B,TNC,SLSQP,dogleg,trust-ncg。如果jac是布尔值并且为True,则假定fun会返回梯度以及目标函数。如果为False,将以数字方式估计梯度。jac也可以是一个可调用的,返回目标的梯度。在这种情况下,它必须接受与fun相同的参数。 hess:可选的,目标函数的Hessian(二阶导数矩阵)或目标函数的Hessian乘以任意向量p。仅适用于Newton-CG,dogleg,trust-ncg。只需要给出hessp或hess中的一个。如果提供了hess,那么hessp将被忽略。如果没有提供hess和hessp,那么将使用jac上的有限差分来近似Hessian乘积。hessp必须将Hessian时间计算为任意向量。 bounds:序列,可选变量的界限(仅适用于L-BFGS-B,TNC和SLSQP)。(min,max)对x中每个元素的对,定义该参数的边界。 constraints:约束,类型有: ‘eq’ for equality, ‘ineq’ for inequality,如:constraints=cons callback(xk):每次迭代召唤函数,需要有参数xk. options : 字典可选, 1.无约束最小化多元标量函数 函数Rosenbrock : 求解: 拟牛顿法的核心思想是构造目标函数二阶导数矩阵黑塞矩阵的逆的近似矩阵,避免了解线性方程组求逆的大量计算,更加高效。介绍:https://blog.csdn.net/jiang425776024/article/details/87602847 函数Rosenbrock : 导数: 求解: 利用黑塞矩阵和梯度来优化,介绍:https://blog.csdn.net/jiang425776024/article/details/87601854 函数Rosenbrock : 构造目标函数的近似二次型(泰勒展开): 利用黑塞矩阵H和梯度做迭代 黑塞矩阵: 实现: 形如: 例子: 实现: leastsq(最小化一组方程的平方和):https://blog.csdn.net/jiang425776024/article/details/86801232 Least-squares(求解带变量边界的非线性最小二乘问题): 形如: 例: 导数: 拟合显示:
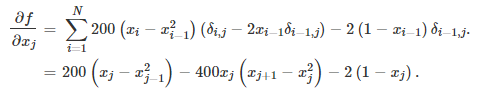




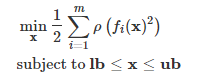

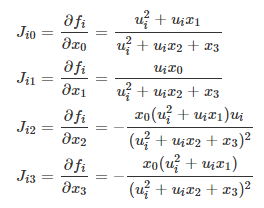

![]()