发布日期:2024-05-13 来源: 网络 阅读量()
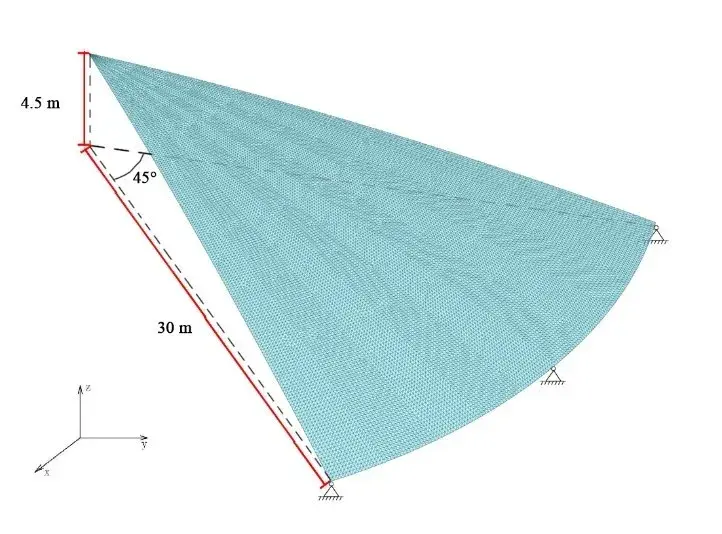
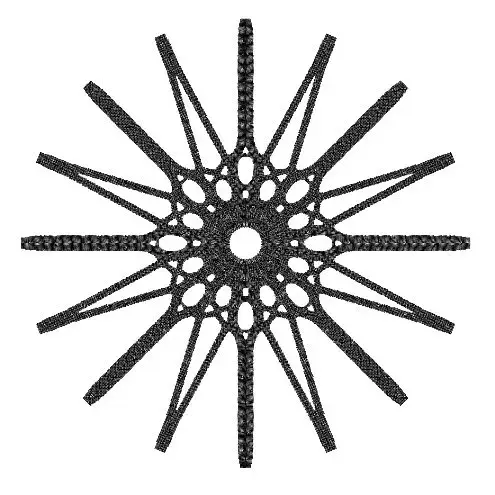
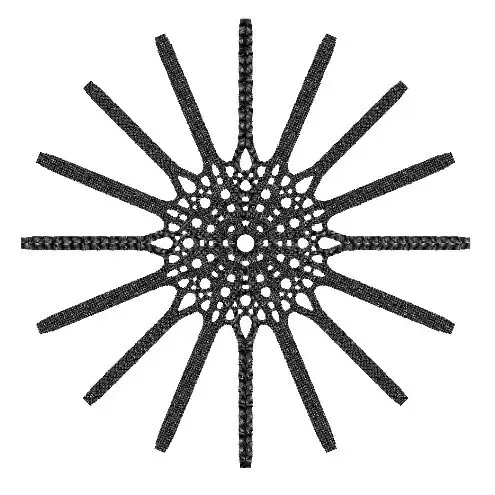
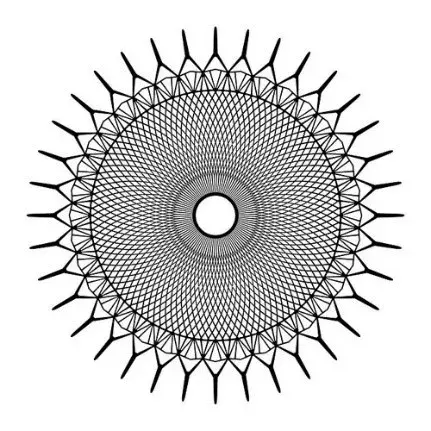
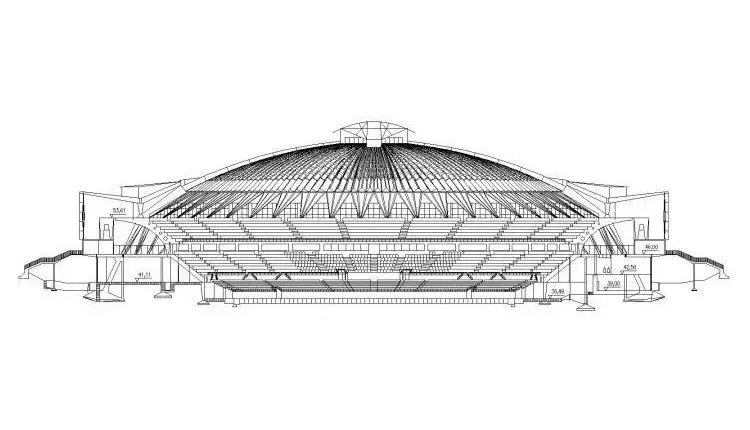
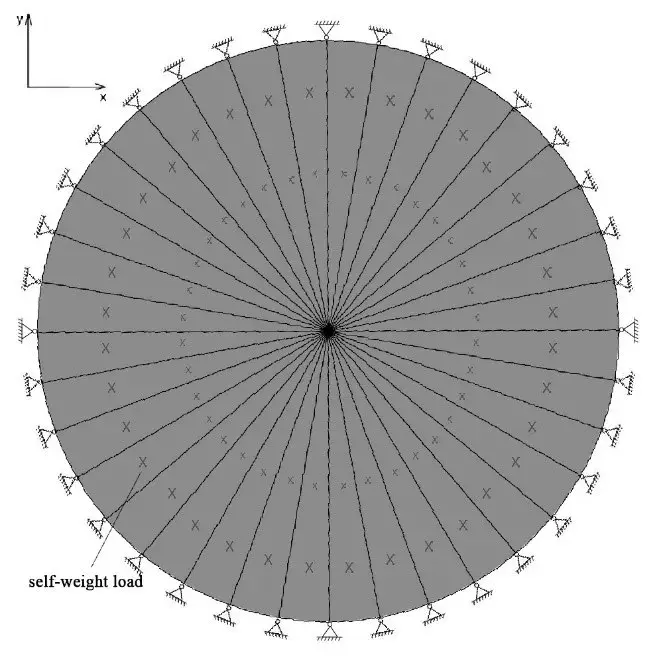
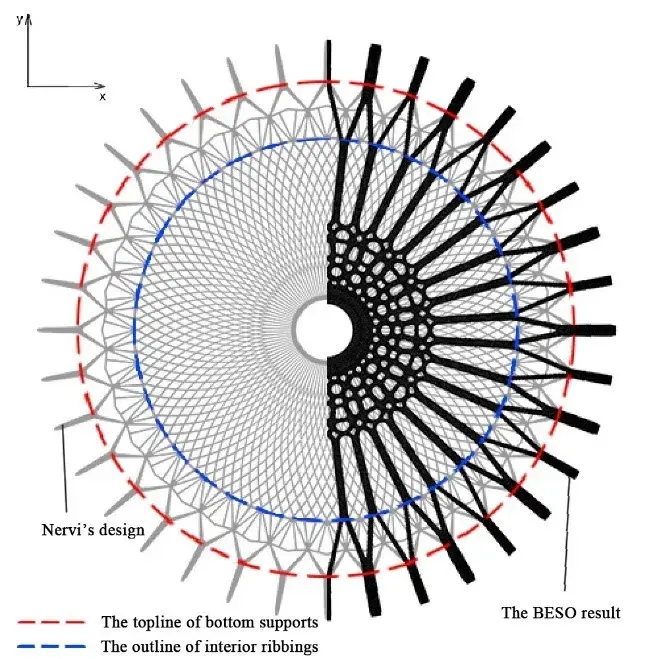
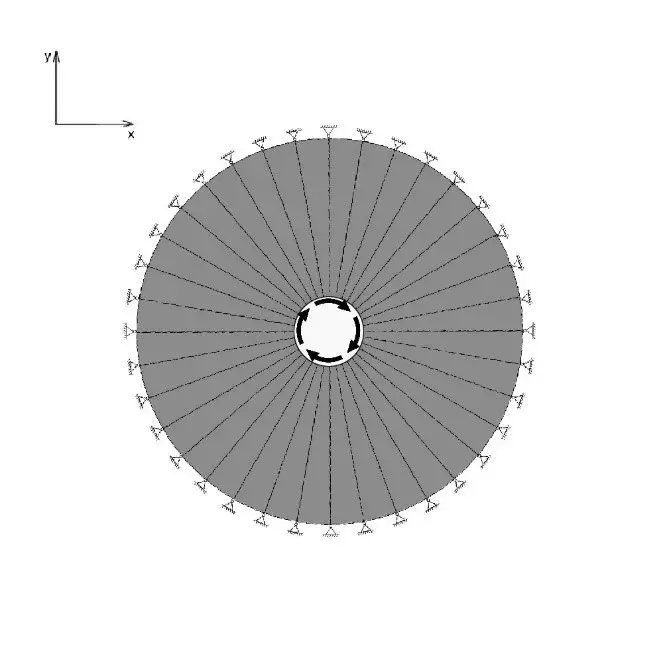
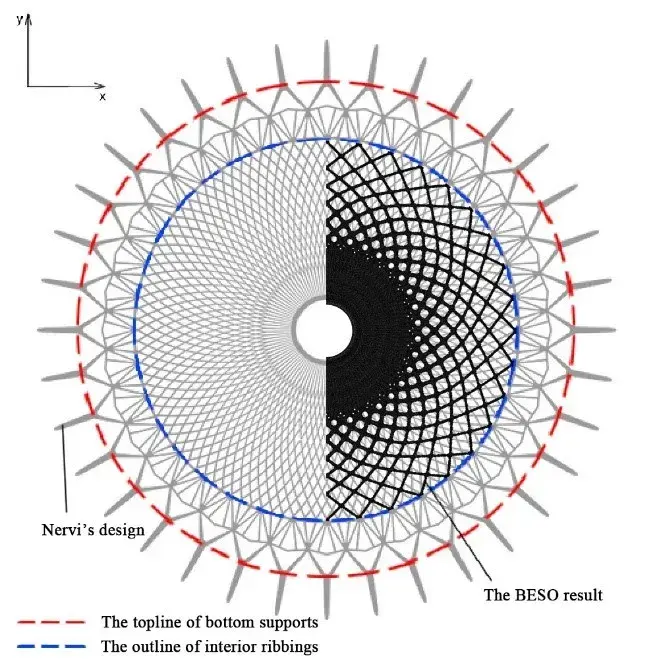
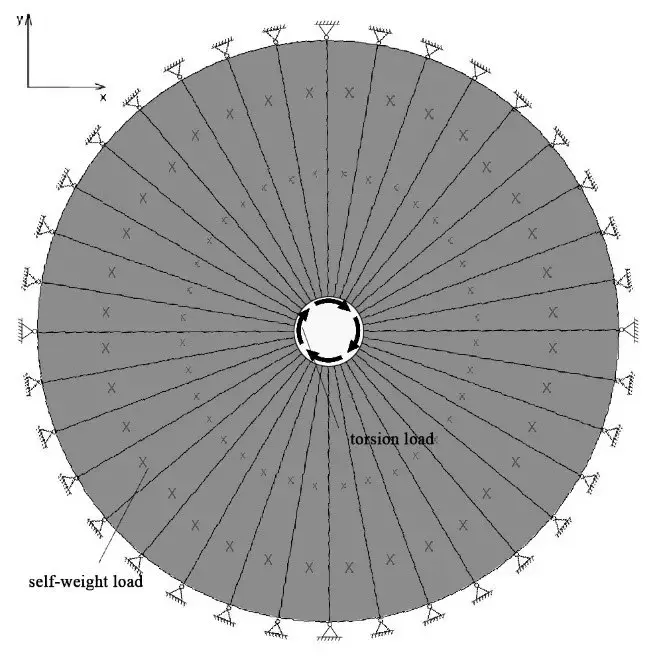
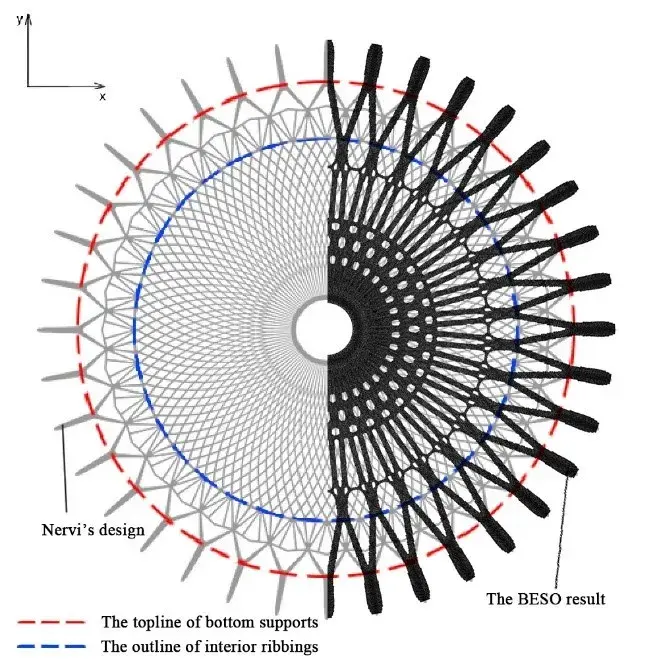
图1:罗马小体育宫 正文 近几年来,得益于计算机技术的飞速发展,薄壳结构由于其高效的结构性能与复杂自由的形态潜力受到了许多建筑师和工程师的青睐。许多建筑和工程研究的学者也开发了诸多壳体找形的算法,比如力密度法[1],推力网格法[2],动态松弛法[3], 弹性粒子系统[4]等等。然而,与上述形状优化(shape optimization)算法不同的是,拓扑优化方法更关注壳面的拓扑关系而不是将它视为一张在演算过程中不会产生新孔洞的连续曲面。这意味着建筑方案设计中的一些功能性开孔,例如窗洞和通风口等,将被纳入到结构优化找形的过程中。同时,拓扑优化形成的美观而高效的方案也可以帮助设计师决策结构体系中需要进行加强加厚或者削弱减材的局部细节。 拓扑优化的目的是在有限的材料用量中找到结构性能较高的材料分配方案。通过近30年的研究,目前已经形成了几种主流的优化方法,它们是渐进结构优化法(ESO)和双向渐进结构优化法(BESO)[5,6],均匀化方法(homogenization method)[7,8],密度法(SIMP)[9,10]和水平集方法(level-set method)[11,12]。其中,由谢亿民院士团队提出的双向渐进结构优化法(BESO)因为其过程简洁、运算高效的特点而被应用于本研究中。 图2:壳体有限元模型和边界条件 如图2所示,由于圆壳结构的对称性,本研究选取了1/8壳体结构作为研究对象。该有限元模型由32230个厚度为0.3m的三角形壳单元构成,其底边缘由三个均匀分布的点支撑,而两条侧边施加了对称性约束,整个结构仅考虑在自重的荷载下进行。实验材料的弹性模量为200GPa,泊松比为0.3,密度为7800 kg/m3。众所周知,壳体是一个对自身形态非常敏感的结构。它的形态与力学性能存在非常密切的关系,有时整体的结构性能甚至会因为局部细微的形态变化而产生巨大的改变。因此,壳结构在进行拓扑优化时,其最终结果与每次迭代中删减材料的量也存在着非常密切的关系。通过研究发现,即使对于相同的初始模型,其拓扑优化结果也会随着渐进率(ER,即每次迭代计算中删减的材料用量)的不同而不同。在本次实验中,我们分别把初始渐进率设置为2%,4%和6%,其结果如图3-图5所示。 图3:自重荷载下的1/8圆壳结构(左)及整体(右)拓扑优化结果(ER=6%, FR=30 mm, VF=30%) 图4:自重荷载下的1/8圆壳结构(左)及整体(右)拓扑优化结果(ER=4%, FR=30 mm, VF=30%) 图5:自重荷载下的1/8圆壳结构(左)及整体(右)拓扑优化结果(ER=2%, FR=30 mm, VF=30%) 虽然上面三种拓扑优化的最终结果外观上截然不同,但它们的结构刚度差异却在0.4%以内,这说明这些结果在工程意义上都是可以被接受的。由此,借助于双向渐进结构优化法,设计师仅仅通过调整不同的参数就可以获得具有相似结构性能而形态各异的多样性壳结构方案。 为了进一步说明拓扑优化在实际工程中的作用,我们特别选择了由意大利著名建筑师、工程师奈尔维(P.L. Nervi)设计的罗马小体育宫(The Palazzetto dello Sport)的圆顶结构进行比对。罗马小体育宫的顶部是一个边缘由36个Y形支柱支撑、直径达60m的混凝土薄壳结构。它的内部以优美的米歇尔桁架(Michell truss pattern)形成交错编织的肋梁进行加强,给人以深刻印象和独特的空间体验(图6)。 图6:罗马小体育宫的结构示意图、剖面图与局部细节 (图片来源: http://www.archidiap.com/opera/palazzetto-dello-sport/ https://www.ciziktirik.com/en/project/sports/palazzetto-dello-sport-section.html) 算例一:在本算例中,基于罗马小体育宫尺寸设计的完整圆形薄壳结构成为了初始设计区域,它同样由36个均匀分布在边缘的点支撑,同时受到了沿z轴负方向的重力作用(图7)。通过图8的对比结果可以看到,在自重作用下的BESO结果同样在边缘附近形成了对应于36个支撑点的Y形支撑,并且尺寸与奈尔维设计的Y形支撑几乎一致。不同的是,在奈尔维的设计中,设计者有意在“过渡区域”(图8中红线与蓝线之间的区域)通过两次分化将节点数量由原来的36增加至108个,而拓扑优化的结果则将边缘的36个节点继承到了“中央区域”(图8蓝线内部)。 图7:算例一的初始设计区域与边界条件示意图 图8:自重作用下BESO优化结果(右半侧)与奈尔维设计(左半侧)对比图 算例二:为了进一步分析奈尔维设计中“中央区域”的结构特征,我们将初始圆形设计区域中蓝线内部对应的部分作为新的设计对象,约束其边缘的36个点并在中心孔洞的边缘施加扭转荷载(图9),进而得到了如图10所示的计算结果。通过对比,我们不难发现在扭转荷载下,圆壳的拓扑优化结果与米歇尔桁架图案保持了高度的一致性。需要指出的是,在本次运算中,由于单元数量的限制,我们只在“中央区域”的边缘约束了36个点,而不是奈尔维设计中的108个点,但不难看出两者的结构逻辑高度相似。 图9:算例二的初始设计区域与边界条件示意图 图10:扭转作用下BESO优化结果(右半侧)与奈尔维设计(左半侧)对比图 算例三:在1956年奈尔维设计罗马小体育宫时期,计算机技术并没有普及,大部分结构设计还是依赖于工程师的经验与分析工作,因此初始的结构方案在设计时通常仅会针对主要的荷载进行分析和设计。通过算例二,我们可以知道罗马小体育宫中央区域的米歇尔图案式分布的加强肋在抵御中心扭转上有着重要的作用。然而,如何同时兼顾地考虑自重和扭转两种荷载的影响,这对于传统的结构设计是一个挑战。幸运的是,在双向渐进结构优化法(BESO)中,我们可以通过简单地施加多工况荷载的方式解决这一难题,将多种荷载同时纳入到结构优化的过程中从而到一个兼顾多种荷载共同作用的优化结果。在算例三中,我们依然沿用原来的圆形设计区域,并且约束了边缘36个点,不同的是,这次我们为模型施加了重力和中心扭转两个荷载(图11),其优化结果如图12。 图11:算例三的初始设计区域与边界条件示意图 图12:多工况作用下BESO优化结果(右半侧)与奈尔维设计(左半侧)对比图 通过对比三个算例的形态,可以看到:仅考虑重力作用时,最终结果主要呈沿半径方向的“直线型”结构,并且孔洞尺寸差异较大,韵律感较差;而仅考虑扭转作用时,优化结果主要由多条一样的“曲线型”结构组成,并且其孔洞尺寸变化平顺,韵律感强;在同时考虑了重力作用和扭转作用后,优化结果在一定程度上继承了重力作用下的“直线型”的结构分布和扭转作用下规整的孔洞分布,为类似圆壳结构设计提供了一种新的思路。 结语 许多传统的壳体找形方法都关注于形状优化而不是拓扑优化,而在本研究中,BESO给建筑师和工程师提供了一种可以快速得到次级结构分布方案的方法。通过简单修改BESO的相关参数,设计者可以快速得到一系列具备同样优秀的结构性能但形态各异的概念方案。同时需要指出的是,虽然本研究关注于薄壳结构的拓扑优化应用,但类似的方法同样适用于其他种类的结构概念设计。