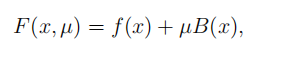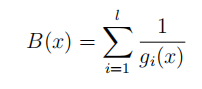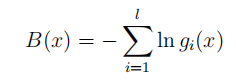发布日期:2024-05-26 来源: 网络 阅读量()
惩罚算法的优点在哪里,“惩罚”这个名字又是怎么来的。
最近做最优化分析需要用到这个,但是发现网上相关文章和浅显的例子都比较少,特别是中文的。自己不算很了解,先稍微解释一下,希望抛砖引玉吧。 惩罚函数,penalty function,用于解决约束条件下的最优化问题。通过惩罚函数可以将有约束的目标函数转化为无约束的目标函数。 举个例子,现在要求函数:f(x)在约束条件g(x)<=0下的最大值。构造函数p(x)=f(x)-h(x)g(x)。其中,h(x)为惩罚项系数函数,可以是函数,也可以是简单的系数,根据约束条件的复杂程度和算法的精度看你什么要求了。 现在取h(x)为正值常数c。p(x)=f(x)-c*g(x),p(x)就是新的目标函数,且不含约束条件。当x取值使得g(x)>0时,p(x)<f(x),无法达到原目标函数原有最大值。-c*g(x)就是惩罚项,当x取值不满足约束条件时,使得目标函数的值远离最优值。 可以看看我的最优化数学笔记,文章专栏更新蹭个回答 惩罚函数可以分为外点法和内点法: 根据约束条件的特点,构造出惩罚惩罚项,然后加入到目标函数中,将其转化为无约束问题 对于如下约束问题: 构造辅助函数,求辅助函数最小值: 惩罚项的需满足条件 1)等式: 目标函数: min f(x) 约束集合: s.t. hi(x)=0 i=1,2,3,...m 增广为外点罚函数: 2)不等式: 目标函数: min f(x) 约束集合: s.t. gi(x)>=0 i=1,2,3,...m 增广为外点罚函数: 3)混合 内点罚函数法的基本思想为在目标函数上引入一个关于约束的障碍项,当迭代点由可行域的内部接近可行域的边界时, 障碍项将趋于无穷大来迫使迭代点返回可行域的内部, 从而保持迭代点的严格可行性。进而将求解约束问题转为求解一系列容易的子问题,从而获得原问题的最优逼近解。方法也称为内点障碍函数法。 目标函数: min f(x) 约束集合: s.t. gi(x)>=0 i=1,2,3,...m 增广为外点罚函数: 障碍函数B(x)一般需满足: (1) 在可行域内连续 (2) 当x趋于g(x)=0的边界,B(x) → ∞.
罚函数方法的基本思想是借助罚函数将约束问题转化为无约束优化问题,进而通过求解一系列无约束最优化问题来获取原约束问题的解。迭代过程中, 罚函数法通过对不可行点施加惩罚,迫使迭代点向可行域靠近。一旦迭代点成为可行点,则这个可行点就是原问题的最优解
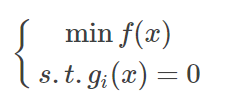
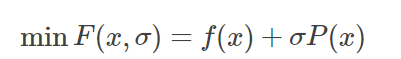
外点法是从可行区外慢慢接近边界,在接近的过程中计算每个阶段极值点,一旦到达可行区范围内,该极值点即为原带约束非线性规划的极值点
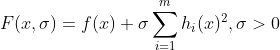
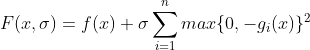
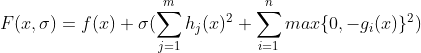

内点罚函数法是一类保持严格可行性的方法,它总是从可行点出发,并保持在可行域内部进行搜索。因而这类方法只适用于只有不等式约束的非线性最优化问题