发布日期:2024-08-12 来源: 网络 阅读量()
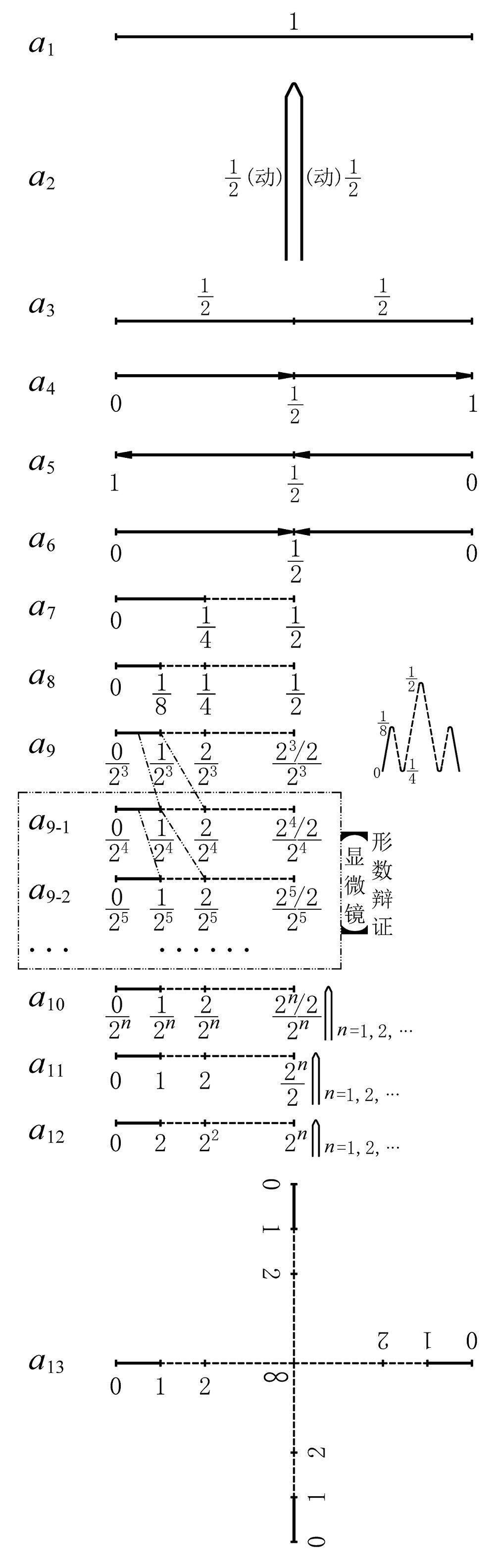
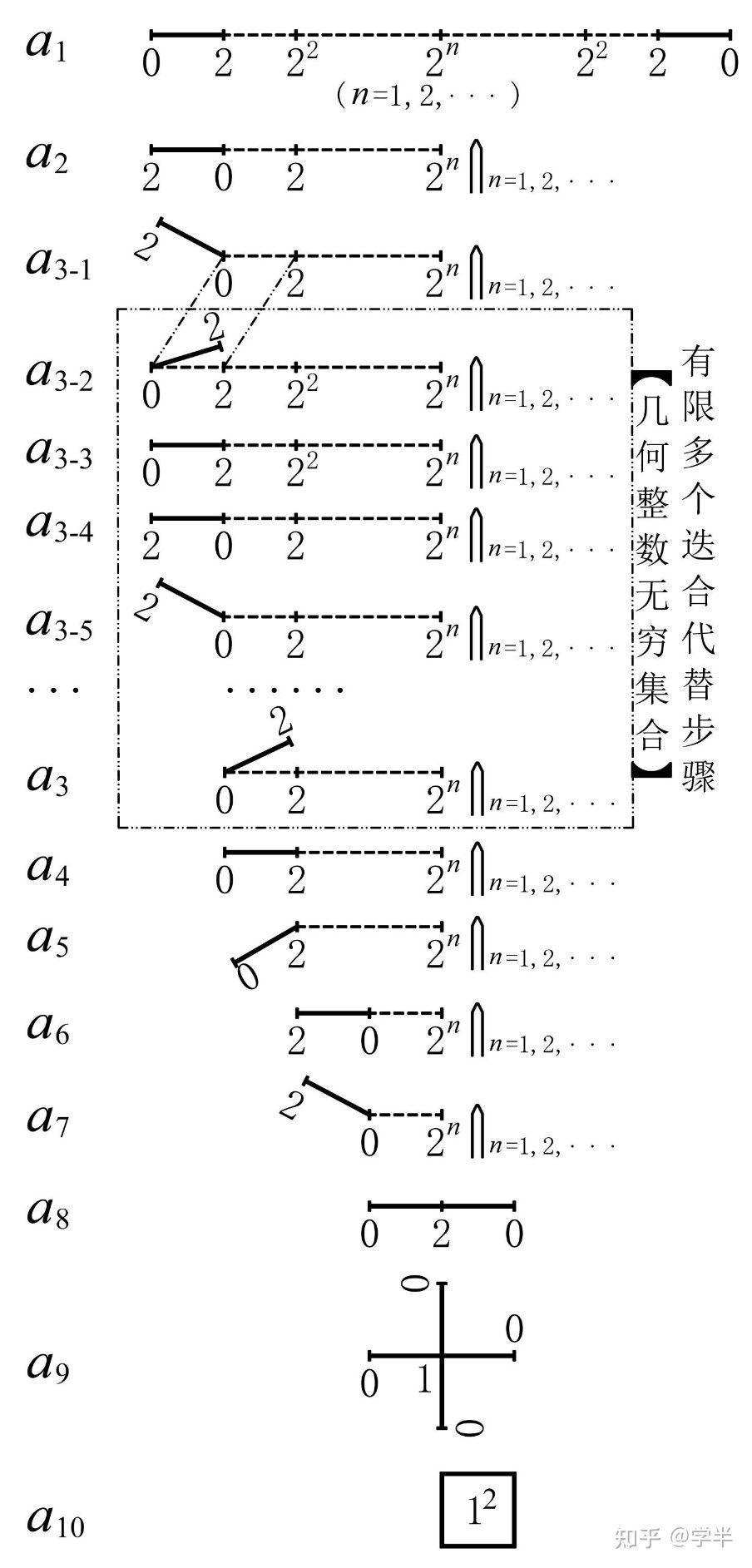
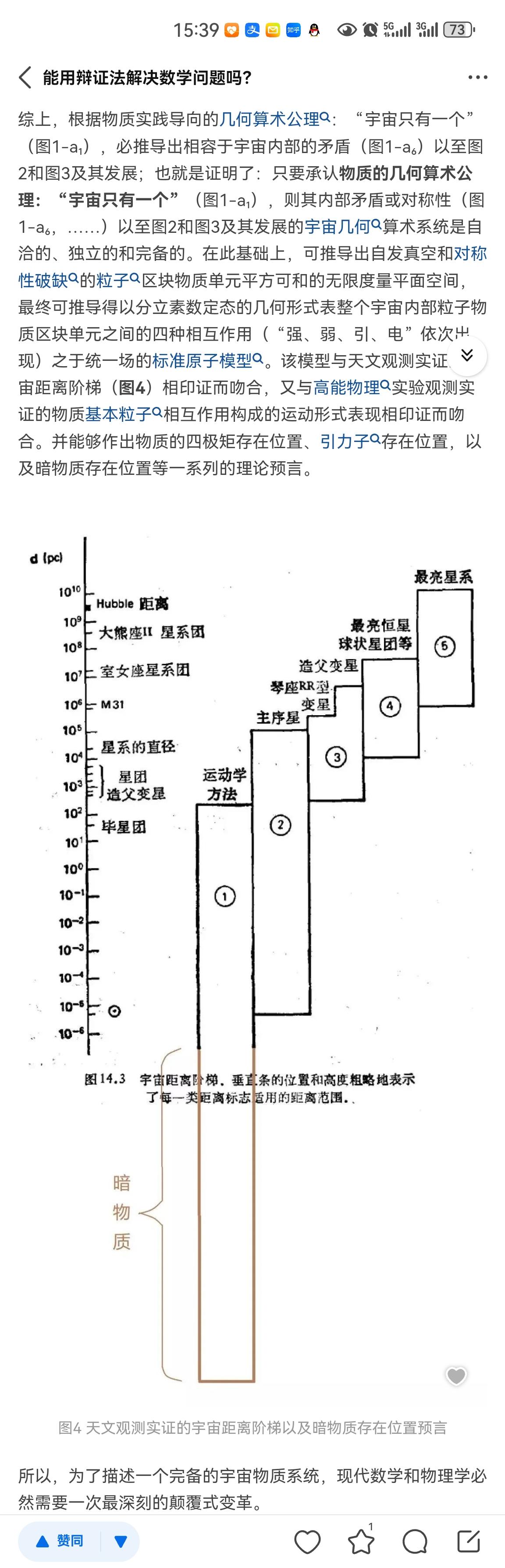
最近看到诺贝尔奖的颁布跟拓扑有关系,我特别好奇拓扑是什么意思呢? 没啥意思,就纯属一个翻译问题,拓扑它的原意是地形地貌,但是在数学上翻译成地形地貌同构貌似总感觉哪里不对劲? – _ – ? 于是就直接音译了。 因为我们要用它来表示,形容三维世界以外的具备类似于形容地形地貌相同抽象特征的意思。 什么地形地貌特征呢?湖泊特征、空缺特征、空洞特征,等等,至于为什么是这个特征,那是因为从一开始的七桥一笔画问题抽象出来的,围起来的那一个个圈就是非常好的特征啦。 以上。 所谓“拓扑”就是把实体抽象成与其大小、形状无关的“点”,而把连接实体的线路抽象成“线”,进而以图的形式来表示这些点与线之间关系的方法,其目的在于研究这些点、线之间的相连关系。表示点和线之间关系的图被称为拓扑结构图。在几何结构中,我们要考察的是点、线之间的位置关系,或者说几何结构强调的是点与线所构成的形状及大小。如梯形、正方形、平行四边形及圆都属于不同的几何结构,但从拓扑结构的角度去看,由于点、线间的连接关系相同,从而具有相同的拓扑结构即环型结构。也就是说,不同的几何结构可能具有相同的拓扑结构。 我的认知拓扑给人视觉是超出三维空间,或是感觉三维空间不合理的存在。最早知道的是日本服装设计师三宅一生用拓扑褶皱设计衣服,感觉效果几何图怪怪的。 拓扑就是一个集合一些子集的集合,这些子集需要满足一些条件,就是拓扑 拓扑空间嘛,就是一个很简洁,很抽象,有点人工感觉的概念。这个概念确实值得深思。一般几何拓扑里几乎感觉不到这个底层概念的存在,很少用到开集闭集,连续映射似乎是出镜率最高的。查里斯基拓扑很有趣。。(格皇的工作,非专业人士就不展开了)。 层,概型这些现代数学十分重要的概念都是在拓扑空间这么个简单抽象,看不出哪里精妙的东西基础上发展出来的。拓扑中的紧致性也很有趣。比如紧群的表示论像极了有限群表示论。(紧,非紧)这一对在空间上和集合论的(有限,无限)有种哲学上的对应,似乎也是说不清为什么的事情。 拓扑空间的重要例子:欧氏拓扑,度量拓扑,查里斯基拓扑,泛函分析的拓扑线性空间,类似于p进线性群上那种拓扑。本人知识有限只知道这些。 作为拓扑概念上的发展有拓扑斯,同样非专业没法多说了。。 拓扑之道立于一。此“一”之形是宇宙的数学物理抽象,表示宇宙所有物质的集合存在。就是说,拓扑理论(包括拓扑概念)建立在公理“宇宙只有一个”的基础上。 拓扑理论(“道”)首先是纯数学上根据公理“宇宙只有一个”构造出来的一种耗散结构,以作为拓扑斯理论的基础。换言之,最简单最基本的拓扑,是刻画整个宇宙的形数结合几何学形式的“一尺之捶,日取其半,万世不竭”,以至于无为而终(宇宙物质量子化的耗散过程之终),终则有始(即无为而无不为,亦即有为)。始——即量子凝聚(收敛或集合)形式宇宙过程的初始条件或边界条件——几何整数微分(其可以被解释为量子物质之间的吸引相互作用出现),这也是拓扑斯理论在严格直观的根基上开始定量演绎和正确发展的基石。详参: 此拓扑及其拓扑斯之“道”最终可成功导出整个宇宙物质的原子论性结构的统一场论粒子物理学模型。
有大神可以详解么,谢谢
___________________________________________