拓扑排序（Topological Sorting）

发布日期：2024-05-20 来源: 网络 阅读量（）

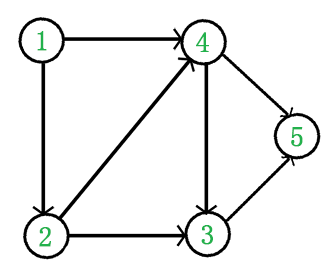
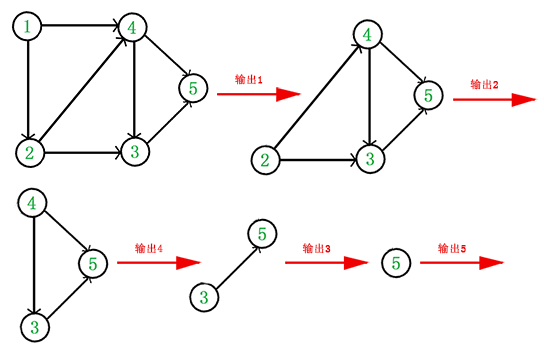
在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

1. 每个顶点出现且只出现一次。
2. 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

例如，下面这个图：

它是一个 DAG 图，那么如何写出它的拓扑排序呢？这里说一种比较常用的方法：

1. 从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。

通常，一个有向无环图可以有一个或多个拓扑排序序列。

拓扑排序通常用来“排序”具有依赖关系的任务。

比如，如果用一个DAG图来表示一个工程，其中每个顶点表示工程中的一个任务，用有向边 <A,B> <script type="math/tex" id="MathJax-Element-1"> </script>表示在做任务 B 之前必须先完成任务 A。故在这个工程中，任意两个任务要么具有确定的先后关系，要么是没有关系，绝对不存在互相矛盾的关系（即环路）。

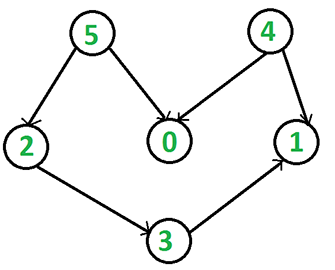
根据上面讲的方法，我们关键是要维护一个入度为0的顶点的集合。

图的存储方式有两种：邻接矩阵和邻接表。这里我们采用邻接表来存储图，C++代码如下：

测试如下DAG图：

输出结果是 4, 5, 2, 0, 3, 1。这是该图的拓扑排序序列之一。

每次在入度为0的集合中取顶点，并没有特殊的取出规则，随机取出也行，这里使用的。取顶点的顺序不同会得到不同的拓扑排序序列，当然前提是该图存在多个拓扑排序序列。

由于输出每个顶点的同时还要删除以它为起点的边，故上述拓扑排序的时间复杂度为 O(V+E) 。

另外，拓扑排序还可以采用 深度优先搜索（DFS）的思想来实现，详见《topological sorting via DFS》。

个人站点：http://songlee24.github.com